Definitions
Let P denote a set of points in the Euclidean plane, not all points on one line; we call such a P a point configuration.
A non-Radon partition of P is a pair {Q, R} of disjoint subsets of P which can be separated by a line, i.e. there is a line s such that Q is contained in one of the open halfspaces determined by s, R is contained in the other open halfspace, and all points of P which are not in R or in Q are on the line s.
A maximal non-Radon partition of P is a non-Radon partition {Q, R} such that all points of P are either in Q or in R.
A maximal non-Radon partition {Q, R} of P is called balanced if the number of points in Q and R differ by at most 1.
Given a point configuration P, we call a line s an elementary line of P of s contains exactly 2 points of P.
The Sylvester-Gallai Theorem states that every point configuration P has an elementary line.
Conjecture
The following conjecture (see Conjecture 4.2 in Ilda P. F. Da Silva, Komei Fukuda: Isolating points by lines in the plane, J. geom. 62 (1998), pp. 48-65) is a strong version of the Sylvester-Gallai Theorem:
Let P be a point configuration and {Q, R} a balanced, maximal non-Radon partition of P. Then there is a crossing elementary line s, i.e. the two points q and r of P which are in s have the property that q belongs to Q and r belongs to R.
Counter-Example
The following counter-example shows that the above conjecture is not valid in general. The example has been found using a database of acyclic oriented matroids of rank 3 (part of the author's Ph.D. thesis; links to database and further information will be added later):
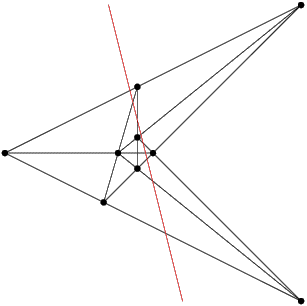 |
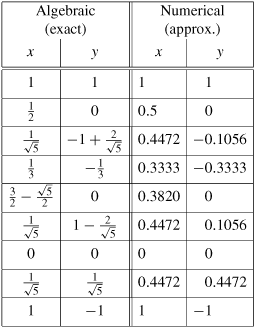 |
| Picture of Counter-Example | Coordinates of Points |
The violating non-Radon partition is e.g. given by the line through the points (0.35, 1) and (0.6,-1), i.e. 8 x + y = 3.8 (this is the red line in the picture above).
The conjecture holds for point configurations with at most 8 points. For 9 points, the above point configuration is (up to isomorphism) the only violating case. An interesting open question is whether the conjecture is true for an even number of points in P, or more general, for which cardinalities of P the conjecture is valid.